During my master thesis is was working on Compressive Sensing algorithms. Compressive Sensing (or Compressed Sampling) is about reconstructing a signal from fewer samples than the signal actually has. This only works when the signal is sparse in some domain.

Now I want to get back into the topic and for this reason I wrote the smallest example for Compressive Sensing that came to my mind. A random sequence of sparse spikes is generated and then I reconstruct the sequence with fewer samples than the original sequence. The signal is sampled by using a normal distributed sampling matrix and the implementation uses the Lasso function of scikit learn.

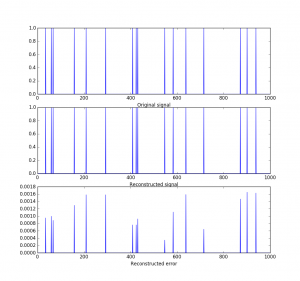
In the following plot you can see the reconstruction of a signal of length 1000 with only 200 samples. An undersampling factor of 200

compressive_sensing_resultsAnd here is the short script written in Python

import numpy as np
from sklearn import linear_model
import matplotlib.pyplot as plt

n=1000 
m=200
percent_zero=0.98
signal = 1.0*(np.random.rand(1, n) > percent_zero)

sampling_scheme = 1.0*(np.random.randn(m, n))

samples = np.dot(sampling_scheme, signal.T)

clf = linear_model.Lasso(alpha=0.001, fit_intercept=False, positive=True)
clf.fit(sampling_scheme, samples)
print("Non zeros original signal: %i" % sum(signal.T > 0))
print("Non zeros reconstructed signal: %i" % sum(clf.coef_ > 0))

plt.subplot(311)
plt.plot(signal.T)
plt.xlabel("Original signal")
plt.subplot(312)
plt.plot(clf.coef_)
plt.xlabel("Reconstructed signal")
plt.subplot(313)
plt.plot((signal-clf.coef_).T)
plt.xlabel("Reconstructed error")

print("Reconstrudtion RMSE: %f" % np.sqrt(np.mean(delta * delta)))

Code is also available on GitHub

Also check out my second post about compressive sensing.